| И.С.Файзуллин, Н.В.Куценко | "Геофизика" № 5 2004 г. |
В методе сейсмической локации бокового обзора (СЛБО) используются рассеянные волны от мелких неоднородностей типа трещин. Однако до последнего времени теоретически не была доказана принципиальная возможность такого применения. Тем не менее на практике выделялись зоны, интерпретируемые как зоны повышенной трещиноватости. В предлагаемой статье на основе численного моделирования впервые обосновывается принципиальная возможность использования рассеянных волн для выделения зон повышенной трещиноватости и предлагается метод их выделения.
Введение
Как показало в ряде работ [2, 4, 5], наиболее адекватной моделью геосреды является модель среды со случайно распределёнными неоднородностями. Затухание упругих волн в такой среде происходит за счёт поглощения в материале пород и рассеяния на неоднородностях. Количественное соотношение этих потерь зависит от структурных особенностей строения пород. В ряде случаев декременты поглощения и рассеяния оказываются одинаковыми [5].
Рассеянные волны в отличие от отражённых и преломленных ещё не нашли широкого применения в сейсморазведке, хотя имеется ряд работ, посвященных их применению для выделения трещиноватых зон. В этих работах указанные выше возможности просто постулируются, а обсуждаются в основном вопросы интерпретации получаемых результатов при решении различных задач. В [1] методом численного моделирования сейсмического поля исследованы отражённые и рассеянные волны от зон диффузной кавернозности и трещиноватости. Однако трещиноватость при этом только предполагается и в расчётной модели никак не учитывается. Кроме того, сравнительно большие размеры (максимальные до 1м) включений типа каверн и большая концентрация микронеоднородностей (до 10% по объёму) позволили в [1] получить рассеянные волны, сравнимые по энергии с отражёнными, что в осадочных породах не наблюдается. Поэтому задача исследования вон, рассеянных от трещиноватых областей, остаётся по-прежнему актуальной. В данной работе методом численного моделирования волновых полей исследуются волны, рассеянные от областей скопления мелких изолированных трещин. Полученные результаты рассмотрены применительно к новому методу локации бокового обзора, но аналогичное исследование может быть проведено и для других методов сейсморазведки.
Методика численного моделирования волновых полей
Моделирование волновых процессов рассеяния проводилось для плоского случая на основе скалярного волнового управления, что не отвечает условиям строгой постановки задачи для твёрдых сред, но позволяет установить основные характеристики рассеяния и выяснить потенциальные возможности различных методов выделения рассеянные волн. При этом рассматривался наиболее интересный для практики случай, когда длина волны больше размеров трещин. Использовался метод моделирования трещин, подробно описанный в [9], который позволяет моделировать области с большой концентрацией трещин, размеры которых меньше шага сетки длины падающей волны. При таком подходе моделирование отдельной трещины не требует задания граничных условий на её поверхности, а сама трещина выступает в виде дипольного источника, форма импульса и амплитуда которого определяются падающей волной. Таким образом, сначала рассчитывается волновое поле без учёта трещин, а затем поле, рассеянное на трещинах. При решении последней задачи общий вклад трещин выражается в виде источника следующего вида:
ssc(x, t)=∑mπa2m(A0(x, xm)qm(t)+A2(x, xm)1/c2∂ttqm(t)+A4(x, xm)1/c4∂ttttqm(t)), (1)
am - половина длины m-й трещины;
c – скорость среды в окрестности m-й трещины;
qm(t)-nm∇pinc(xm, t);
pinc – поле, рассчитанное без учёта трещин; xm – координаты центра m-й трещины;
nm – вектор нормали к поверхности m-й трещины. Коэффициенты A0, A2, A4 не зависят от времени и быстро убывают от центра трещины xm. Их вид представлен в работе [9]. Таким образом, поле, рассеянное на трещинах, обозначим его psc, может рассчитываться отдельно от поля pinc. Очевидно, что полное поле p = pinc+psc. Возможность получения рассеянного поля отдельно от падающего имеет принципиальное значение, так как при этом эффекты рассеяния могут быть исследованы наиболее полно.
Для поучения рассеянного поля прямую задачу приходится решать дважды: первый раз – для расчёта волнового поля в отсутствие трещин, второй – для расчёта поля, рассеянного на трещинах. Математически обе задачи формулируются следующим образом:
ptt = c2Δp+s(x,t), (2)
где s(x,t) – источник; c – скорость распространения волн; Δ - оператор Лапласа;
p(x,t) – волновое поле; x = (x,z). В первом случае, при расчёте pinc, s(x,t) задаётся произвольно (например, импульс Риккера), во втором, при расчёте psc, определяется формулой (1).
Для аппроксимации уравнения (2) используется конечно-разностная схема, предложенная в работе [7]. Данная схема имеет четвёртый порядок аппроксимации по временной координате, десятый по пространственным координатам и записывается следующим образом:
pn+1=-pn-1+2pn+c2Δt2⟨(∂2pn/∂x2)+(∂2pn/∂z2)⟩+c4Δt4/12 ⟨ ∂4pn/∂x4 + 2(∂4pn/∂x2∂z2)+∂4pn/∂z4⟩. (3)
Вторая производная по пространственной координате в (3) заменяется следующим выражением:
∂2pi/∂x2=1/Δx2 ⟨ ω0pi+∑5k=1ωk(pi+k+ pi-k⟩ (4)
Значения коэффициентов ωk в (4) приведены в работе [7].
Для того чтобы свести отражения волн от границ сетки к минимуму, применяются два типа граничных условий. Сначала волновое уравнение на границе области заменяется параксиальным волновым уравнением, описывающим распространение волн лишь в одном направлении [6, 8]
∂p/∂t+c(∂p/∂x)=0; (5)
Такая замена обеспечивает достаточное поглощение вон лишь в направлении нормали к границе области. Затем применяются условия поглощения, подробно описанные в работе [10]. Для правой границы, например, они выглядят следующим образом:
∂2p/∂t2=c2 ⟨ ∂2p/∂x2+∂2p/∂z2 ⟩ - ε(x)⟨ ∂p/∂t+c(∂p/∂x) ⟩, (6)
где ε(x) – коэффициент затухания.
Применение двух типов поглощения граничных условий позволяет минимизировать энергию волн, отражённых от границ вычислительной области.
Моделирование рассеяния волн от областей со случайно распределёнными трещинами
Моделирование проводилось на сетке с шагом по пространственным координатам Δx = Δz = 5 и по временной координате Δt = 0,001 c. размер сетки равнялся 300x300 точек по координатам x и z соответственно, скорость распространения волн была равна 2500 м/c. В области с трещинами каждый узел сетки содержал трещину, длина которой менялась случайным образом от 1 до 200см, также случайно менялась ориентировка трещин. В первом приближении такая область соответствовала модели среды со случайно распределёнными трещинами. Размеры областей рассеяния (здесь и в дальнейшем так обозначаются области с трещинами) приведены в таб.1. Схема проведения экспериментов представлена на рис.1. Центры областей рассеяния на всех моделях находятся в центре вычислительной сетки. Положение излучателя относительно верхней границы области менялось для каждой модели так, чтобы расстояние от излучателя до верхней границы области рассеяния оставалось постоянным. В качестве импульса падающей волны (далее называется зондирующим импульсом) использовался импульс Риккера с доминирующей частотой 25 Гц.
Таблица 1
Параметры области с трещинами для различных моделей
| Модель | Размер области рассеяния | Число трещин |
|---|
| 1 | 50 x 50 м | 121 |
| 2 | 100 x 100 м | 441 |
| 3 | 200 x 200 м | 1681 |
| 4 | 1450 x 30 м | 2037 |
Волновые картинки для четырёх моделей приведены на рис.2 (см. цвет. вкл.) , вид рассеянных импульсов и соответствующие им амплитудные спектры – на рис.3 (а, б, в, г,). На этом же рисунке показан зондирующий импульс и соответствующий ему амплитудный спектр. Рассеянные назад импульсы регистрировались в точке изучения, рассеянные вперёд и зондирующий – в точке, симметричной положению излучателя относительно центра области рассеяния.
Как уже отмечалось выше, рассеянное и падающее поля рассчитываются отдельно, поэтому получение сравнительных оценок амплитуд рассеянных импульсов не представляет затруднений (таб.2). При этом сравнение проводилось через амплитуду импульса в падающей волне, регистрируемой в той же точке, что и импульс волны, рассеянной вперёд. Как видно из табл.2, максимальная амплитуда импульса рассеянной назад волны практически не зависит от размеров области рассеяния (см. табл.1), за исключением модели 1, на которой указанная область в отличие от остальных моделей занимает треть зоны Френеля по горизонтали. Длительность импульса рассеянной назад волны увеличивается с увеличением размеров области рассеяния по вертикали (см. рис.3).
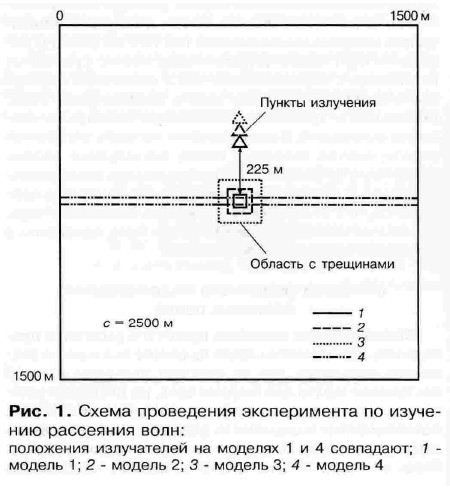
Рис. 1
Схема проведения эксперимента по изучению рассеяния волн:
положения излучателей на моделях 1 и 4 совпадают; 1 - модель 1; 2 - модель 2; 3 - модель 3; 4 - модель 4
Это можно объяснить тем , что в формировании рассматриваемой волны непосредственно участвуют все участки области рассеяния с соответствующим сдвигом во времени. Как видно из рис.3, максимум амплитудного спектра импульса рассеянной назад волны на моделях 1, 2, 3 смещается в область высоких частот одинаково, примерно на 5-7 Гц, а на модели 4 такого смещения не наблюдается, что может быть связано с большой протяжённостью области рассеяния по горизонтали. Следовательно, рассеяние на высоких частотах происходит более интенсивно, но без зависимости от размеров области рассеяния по вертикали.
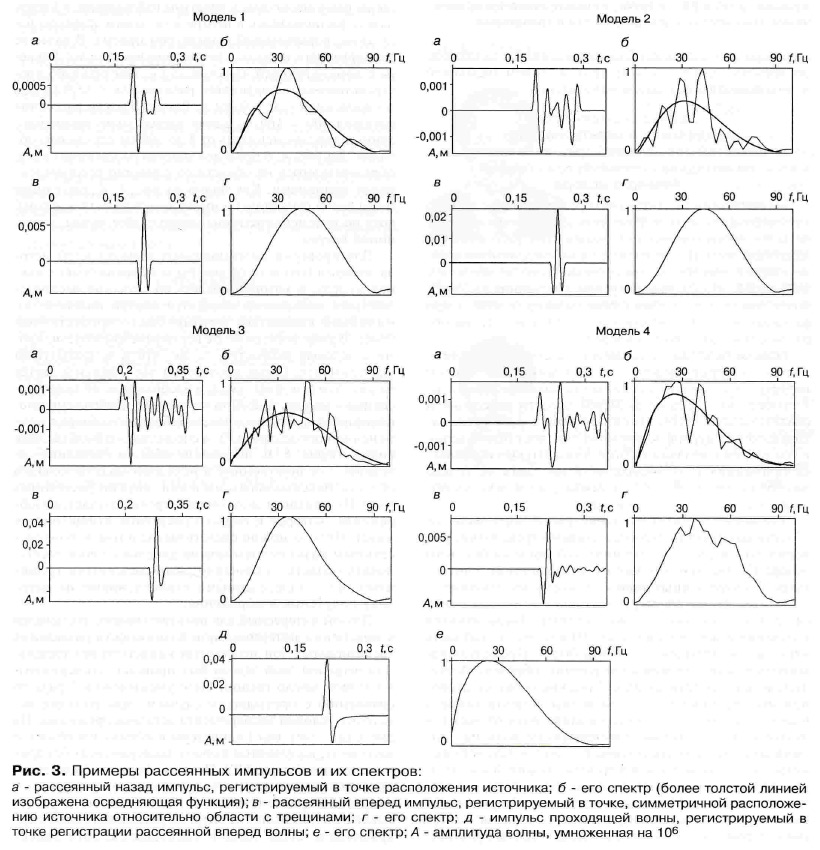
Рис.3
Примеры рассеянных импульсов и их спектров:
а - рассеянный назад импульс, регистрируемый в точке расположения источника; б - его спектр (более толстой линией изображена осредняющая функция); в - рассеянный вперед импульс, регистрируемый в точке, симметричной расположению источника относительно области с трещинами; г - его спектр; д - импульс проходящей волны, регистрируемый в точке регистрации рассеянной вперед волны; е - его спектр; А - амплитуда волны, умноженная на 106
Совершенно по-другому происходит образование и распространение рассеянной вперёд волны. Как видно из рис.3 и таб.2, максимальная амплитуда импульса возрастает с увеличением размеров области рассеяния (см. табл.1), смещение максимумов амплитудного спектра зависит от размеров указанной области, однако длительность импульса остаётся практически одинаковой на всех моделях.
Рассмотренные выше особенности волн могу быть объяснены тем, что рассеянные вперёд волны образуются по мере продвижения падающей воны, распространяющейся в том же направлении и стой же скоростью, а образование рассеянной волны происходит на разных участках области рассеяния с задержкой во времени, определяемой прохождением падающей волны в противоположном направлении.
Таблица 2
Отношение максимальных амплитуд импульсов различных волн
| Отношение амплитуд | Модель 1 | Модель 2 | Модель 3 | Модель 4 |
|---|
| АПВ/АРВ | 52,5 | 15,8 | 7,6 | 45,6 |
| АРВ/АРН | 5,44 | 10,8 | 23,4 | 3,57 |
| АПВ/АРН | 285,6 | 170,6 | 177,8 | 162,8 |
Примечание: РВ – рассеянная вперёд, РН – рассеянная назад, а ПВ – падающая волна, РН – измерена в точке излучения, а ПВ и РВ – в точке, симметричной точке излучения относительно центра области с трещинами.
Оценка возможности выделения и оконтуривания областей повышенной трещиноватости по методике сейсмической локации бокового обзора
На основании рассмотренных результатов численного моделирования нельзя проводить количественные расчёты по соотношению интенсивностей рассе6йнных и падающих волн. Из сопоставления на качественном уровне следует, что волны, рассеянные назад от области с небольшой концентрацией трещин (1 трещина на 25 м2), более чем на два порядка слабее падающих волн, а при размерах области, превышающих длину волны, на порядок слабее рассеянных вперёд.
Однако рассеянные назад волны обладают особенностью, которая представляет большой практический интерес. Эта особенность связана с зависимостью длительности импульса от размеров области рассеяния и свидетельствует о том, что вклад участков области, находящихся за первой зоной Френеля, достаточно велик и соизмерим с вкладом от этой зоны. Отсюда появляется принципиальная возможность выделять не только начальную часть области рассеяния, но и всю эту область, т.е. определять её контуры.
Указанная особенность волн, рассеянных назад от области со случайно распределёнными трещинами, уже используется в методе сейсмической локации бокового обзора [3]. Однако, как уже отмечалось выше, ещё остался ряд нерешённых вопросов по его применению.
В этом методе апертуры излучения и приёма выносятся за область исследуемого объёма. Число пунктов излучения и приёма достигает 100 и более, а кратность накопления сигналов – 10 000 и более. Процедура накопления осуществляется следующим образом. Исследуемый массив длится на кубические блоки со стороной меньше половины длины волны, в центр каждого блока осуществляется фокусирование волн от всех излучателей с синфазным суммированием волн на приёмниках от каждого излучения, т.е. амплитуды всех импульсов, приводящих в центр кубического блока и от центра блока ко всем приёмникам, суммируются и возводятся в квадрат. Поскольку колебания не гармонические, получаемую величину условно можно назвать энергией рассеянной волны, как это и делается на практике. Каждому блоку приписывается полученное значение энергии, по максимальным значениям которой выделяют область рассеяния.
В отличие от отражённых и преломленных, рассеянные назад волны не выделяются на сейсмограммах, что ставит под сомнение сам факт их существования. Поэтому было интересно увидеть их на моделях с использованием методики наблюдений, аналогичной методике локации бокового обзора, что и было осуществлено во втором эксперименте. На рис.4, а (см. цвет. вкл.) приведена схема эксперимента, которая отображает систему наблюдений в методе локации бокового обзора для плоского случая. В эксперименте 60 приёмников были размещены равномерно вдоль апертуры наблюдения, а 3 излучателя располагались в центре и по краям апертуры излучателя, совмещённой с апертурой приёма. В качестве зондирующего импульса использовался импульс Риккера с доминирующей частотой 25 Гц, шаг сетки по пространственным координатам равнялся Δx = Δz = 10 м, а по временной - Δt = 0,001 с. Размер области рассеяния составил 400 x 160 м, длина произвольно ориентированных трещин менялась от 1 до 500 см случайным образом. На рис.4, б приведён пример рассеянного поля, образовавшегося на области со случайно распределёнными трещинами. Как видно из рис.4 б, рассеянная назад волна существует и имеет довольно чёткий фронт, хотя по интенсивности она много слабее волны, рассеянной вперёд.
Для проверки потенциальных возможностей метода локации бокового обзора была выбрана более сложная модель, в которой область со случайно распределёнными трещинами находится внутри плата с пониженной скоростью, имитирующего продуктивный пласт. В этом эксперименте все параметры модели, кроме пластовых скоростей, те же, что и в предыдущем эксперименте. Схема проведения эксперимента даётся на рис.5, а ( см. цвет. вкл.), а изображение области рассеяния – на рис.5, б. При поучении изображения использовалась методика локации бокового обзора с применением процедуры АРУ и специального фильтра. Как видно из рис.5, б, положение области рассеяния совпадает с её положением в исходной модели только в области максимальных значений энергии рассеянных волн. По меньшим значениям энергии получается изображение, которое к области рассеяния отношения не имеет. Отсюда можно сделать вывод том, что по рассеянным назад волнам можно довольно точно восстановить область со случайно распределёнными трещинами, но с определёнными ограничениями на методику получения изображения.
Другой интересный для практики вопрос заключается в выяснении потенциальной возможности разделения трещиноватых зон по степени концентрации трещины. Для решения этой задачи был проведён эксперимент, в котором число трещин было уменьшено в 2 раза по сравнению с предыдущим случаем, при этом все остальные условия эксперимента остались прежними. На рис.6 (см цвет. вкл.) приведены изображения областей рассеяния, полученные в обоих экспериментах без применения процедуры АРУ. Поэтому форма изображения, представленного на рис.6, а, несколько отличается от полученной ранее (см. рис.5, б). Как видно из рис.6 максимальное значение энергии рассеянных волн с сокращением числа трещин уменьшается.
К статье "О возможности применения рассеянных волн для изучения трещиноватости геосреды по данным численного моделирования"

Рис. 2
Поля рассеянных волн на областях со случайно распределёнными трещинами в момент времени t=0,35 с
|

Рис. 4
Схема проведения эксперимента (а) по наблюдению рассеянных волн и волновая картина, полученная в момент времени t=0,75 с (б)
|
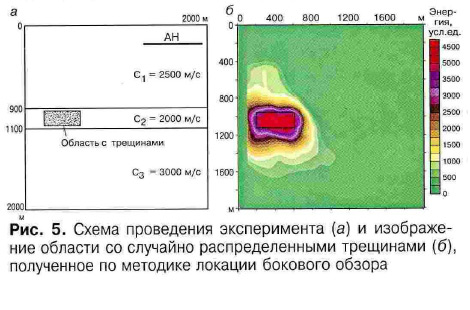
Рис. 5
Схема проведения эксперимента (а) и изображение области со случайно распределёнными трещинами (б), полученное по методике локации бокового обзора
|
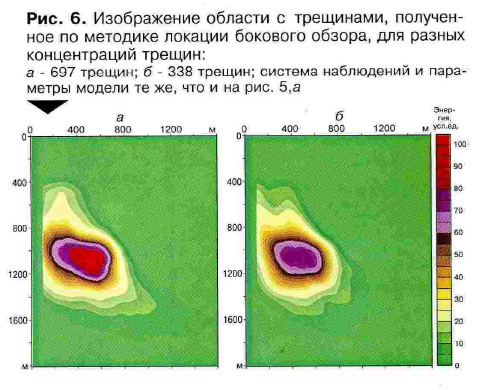
Рис. 6
Изображение области с трещинами, полученное по методике локации бокового обзора, для разных концентраций трещин
|
Скачать:  О возможности применения рассеянных волн для изучения трещиноватости... (PDF, 1.08 Mb) О возможности применения рассеянных волн для изучения трещиноватости... (PDF, 1.08 Mb) |